El Proyecto Educativo Nacional
plantea transformar nuestras instituciones educativas en lugares efectivos,
agradables e integradores, que ofrezcan una educación básica de calidad, donde
todos los jóvenes logren los aprendizajes fundamentales a que tienen derecho.
En esa perspectiva, la política educativa que viene implementando el Ministerio
de Educación ha considerado como una de sus prioridades la mejora de los
aprendizajes matemáticos. Necesitamos ampliar y consolidar el desarrollo de
competencias y capacidades matemáticas que son reconocidas en todos los
sistemas educativos del mundo, como una de los pilares del desarrollo de las
sociedades en el siglo XXI.
La educación matemática, de cara
a la dinámica actual del desarrollo de nuestra sociedad, representa una
actividad humana que afronta cada día nuevos retos y oportunidades. Han surgido
en nuestra época nuevos enfoques y paradigmas en todas las formas de aprender y
desarrollar las matemáticas, que están induciendo a la Educación matemática a
enfrentar con otros ojos situaciones inevitables, derivadas de los avances
científicos y tecnológicos, con sus consiguientes cambios de concepción y
mentalidad.
Las sociedades tienden a ser más
dinámicas y competitivas, aunque a la vez más desiguales, demandando de
nuestras nuevas generaciones una mejor preparación para afrontar retos personales,
sociales y de grupo como país. En ese sentido, necesitamos transitar como país
a una situación de mayor acceso, manejo y aplicación de conocimientos, donde la
educación matemática se convierte en un valioso factor de su desarrollo
económico, científico, tecnológico y social. Insertarnos en la sociedad del
conocimiento implica propiciar en todos los ciudadanos un rol activo, crítico,
creativo y emprendedor, así como oportunidades para aprender a hacer uso de sus
capacidades de forma pertinente a los distintos contextos que deben afrontar
(UNESCO, 2005).
Por las consideraciones
señaladas, la educación matemática peruana, en el presente y en el futuro
inmediato, requiere centrar sus esfuerzos en promover el desarrollo de
competencias y capacidades para aprender a aprender matemática y así puedan ir
avanzando e integrándose al ritmo con el que caminan las otras dimensiones de
la vida social.
El presente documento contiene
tres capítulos. En el primer capítulo, se presentan algunas aproximaciones
teóricas relacionadas con el aprendizaje y el aprender a aprender matemáticas.
La matemática siempre ha desempeñado un rol
fundamental en el desarrollo de los conocimientos científicos y tecnológicos.
En ese sentido, reconocemos su función instrumental y social que nos ha
permitido interpretar, comprender y dar soluciones a los problemas de nuestro
entorno.
En efecto, todos los seres humanos, desde que
nacemos hasta que morimos, usamos algún tipo de aprendizaje matemático. Nacemos
sin saber matemáticas, pero el mundo está lleno de experiencias que pueden
convertirse en aprendizajes matemáticos utilizables en diversas circunstancias.
Así, el niño que cuenta los dedos de su mano por primera vez, sabrá que en cada
mano tiene cinco. Esto no lo exime de cometer errores al contar una y otra vez
sus dedos, sin embargo ayuda a aprender.
Además de las experiencias cotidianas que
ayudan a aprender matemáticas, contamos con instituciones educativas, en donde
se accede a una educación matemática formal. Se aprende a comprender y producir
textos matemáticos, a razonar matemáticamente, a resolver problemas
matemáticos, etc.
En algunos casos al terminar la educación
básica, se continúa con el aprendizaje de la matemática en la educación
superior. El aprendizaje de la matemática es interminable, por lo que muchos
eruditos, haciendo honor a la tradición socrática, declararon que mientras más
se aprende matemáticas, más falta por aprender.
El problema es cuando la matemática que
aprendemos resulta poco significativa, poco aplicable a la vida, o simplemente
aburrida, tanto que al dejar el colegio olvidamos lo que aprendimos y no seguimos
aprendiéndola por nuestra cuenta. Si bien hay quienes aprenden la matemática
por sí mismos, la mayoría no lo hace. Necesitamos algún tipo de acompañamiento
para aprender matemática y reflexionar sobre nuestro aprendizaje. Es en la
educación matemática formal donde se puede ofrecer una intervención pedagógica
que nos posibilite tal desarrollo.
APRENDER
A APRENDER MATEMÁTICAS
¿Cómo
tener estudiantes motivados a aprender matemáticas y mucho más, a aprender a
aprender matemáticas por sí mismos? Requerimos ambientes educativos que brinden
confianza y tranquilidad y donde reine el respeto mutuo, la tolerancia y la
libertad. Donde se puedan generar dinámicas de aprendizajes significativos y
de reflexión crítica con el fin de que se propicie el aprender y el aprender a
aprender matemáticas de manera fácil y profunda para utilizar los conocimientos
matemáticos en diversas situaciones, no sólo en el ámbito escolar sino también
fuera de él.
El
aprender a aprender matemáticas implica aprender a ser perseverante y autónomo
en la organización de nuestros aprendizajes, conllevando a un nivel de control
estratégico que reconozca experiencias, conocimientos previos, valores e
implicancias de diversas índoles, haciendo que nuestros estudiantes sean
eficaces en la construcción de sus conocimientos y la toma de decisiones. En la
escuela la promoción de la competencia matemática se suscita entorno a las
capacidades de matematizar, elaborar y seleccionar estrategias, a representar
matemáticamente situaciones reales, a usar expresiones simbólicas, a comunicar
y argumentar, a explorar, probar y experimentar.
Si
los estudiantes adquieren estas capacidades y las usan en su vida, adquirirán
mayor seguridad y darán mayor y mejor sentido a su aprendizaje matemático. La matemática
cobra mayor significado y se aprende mejor cuando se aplica directamente a
situaciones de la vida real. Nuestros estudiantes sentirán mayor éxito cuando
pueden relacionar cualquier aprendizaje matemático nuevo con algo que saben y
con la realidad cotidiana. Esa es una matemática para la vida, donde el
aprendizaje se genera en el contexto de la vida y sus logros van hacia ella.
Desarrollar
habilidades de independencia y control sobre el proceso de aprendizaje exige
que los estudiantes reflexionen sobre su propio aprendizaje, sean conscientes
sobre cómo aprenden, practiquen el auto cuestionamiento y usen de forma
abierta, atrevida y flexible diversas estrategias para aplicar selectivamente
en la ejecución de determinadas tareas y actividades matemáticas. Por ello, es
importante el rol del docente como agente mediador, orientador y provocador de
formas de pensar y reflexionar durante las actividades matemáticas.
Las
habilidades matemáticas requieren constancia, práctica sistemática y deliberada
para poder ser transferidas y utilizadas en diversos contextos escolares y
fuera de ellos. Además, las oportunidades de practicar dentro de la
institución educativa dependen de nuestro apoyo activo.
COMPETENCIA MATEMÁTICA
- La competencia matemática en la Educación
Básica promueve el desarrollo de capacidades en los estudiantes, que se
requiere para enfrentar a una situación problemática en la vida cotidiana.
Alude, sobre todo, a una actuación eficaz en diferentes contextos reales a
través de una serie de herramientas y acciones. Es decir, a una actuación
que moviliza e integra actitudes.
- La competencia matemática es entonces un
saber actuar en un contexto particular, que nos permite resolver
situaciones problemáticas reales o
de contexto matemático.
- Un
actuar pertinente a las características de la situación y a la
finalidad de nuestra acción, que selecciona y moviliza una diversidad de
saberes propios o de recursos del entorno, a través de procedimientos que
satisfagan determinados criterios básicos.
“Como una alternativa
a los modelos formativos tradicionales de aprendizaje memorístico de
matemática, los cuales difícilmente pueden ser aplicados a la vida real, surge
la competencia matemática”
CRITERIOS BASICOS
a) Un saber actuar: Alude
a la intervención de una persona sobre una situación problemática determinada
para resolverla, pudiendo tratarse de una acción que implique sólo actividad
matemática.
b) En un contexto particular: Alude a una situación problemática real o
simulada pero plausible que establezca ciertas condiciones y parámetros a la
acción humana, y que deben tomarse en cuenta necesariamente.
c) Un actuar pertinente: Alude a la indispensable correspondencia de
la acción con la naturaleza del contexto en el que se interviene para resolver
la situación problemática. Una acción estereotipada que se reitera en toda
situación problemática no es una acción pertinente.
d) Que selecciona y moviliza saberes: Alude a una acción que echa mano de los
conocimientos matemáticos, habilidades y de cualquier otra capacidad matemática
que le sea más necesaria para realizar la acción y resolver la situación
problemática que enfrenta.
e) Que utiliza recursos del entorno: Alude a una acción que puede hacer uso
pertinente y hábil de toda clase de medios o herramientas externas, en la
medida que el contexto y la finalidad de resolver la situación problemática lo
justifiquen.
f) A través de
procedimientos basados en criterios: Alude a formas de
proceder que necesitan exhibir determinadas características, no todas las
deseables o posibles sino aquellas consideradas más esenciales o suficientes
para que logren validez y efectividad.
FORMULACIÓN
DE LA COMPETENCIA MATEMÁTICA
En
la formulación de una competencia matemática necesita visibilizarse:
·
La acción
que el sujeto desempeñará
·
Los
atributos o criterios esenciales que debe exhibir acción
·
La
situación, contexto o condiciones en que se desempeñará la acción
EJEMPLO:
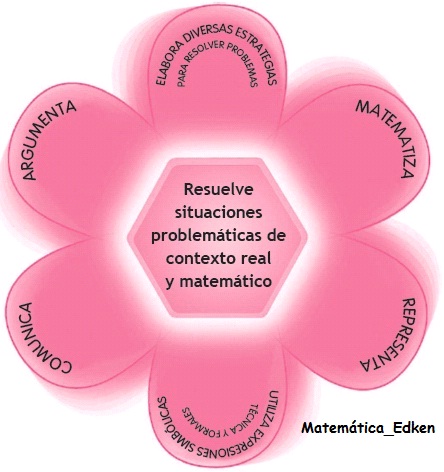
En
la competencia matemática « Resuelve situaciones problemáticas de contexto real
y matemático que implican la construcción del significado y el uso de los
números y sus operaciones empleando diversas estrategias de solución,
justificando y valorando sus procedimientos y resultados », puede
distinguirse:
RESOLUCIÓN DE
SITUACIONES PROBLEMÁTICAS COMO COMPETENCIA MATEMÁTICA
La
resolución de situaciones problemáticas reales es la competencia matemática del
Área de Matemática. El estudiante la desarrollará durante su experiencia
escolarizada y no escolarizada a lo largo de toda su vida.
Se
ha definido cuatro competencias matemáticas en términos de resolución de
problemas, que atraviesan toda la Educación Básica. Competencias que suponen un
desempeño global y que corresponden a los cuatro dominios del Área de
Matemática:
CAPACIDADES
MATEMÁTICAS
La
resolución de situaciones problemáticas es entonces una actividad matemática
importante que nos permite desarrollar capacidades matemáticas. Todas ellas
existen de manera integrada y única en cada persona y se desarrollan en el
aula, la escuela, la comunidad, en la medida que dispongamos de oportunidades y
medios para hacerlo.
En
otras palabras, las capacidades matemáticas se despliegan a partir de las
experiencias y expectativas de nuestros estudiantes, en situaciones
problemáticas reales. Si ellos encuentran útil en su vida diaria los
aprendizajes logrados, sentirán que la Matemática tienen sentido y pertinencia.
La
propuesta pedagógica para el aprendizaje de la matemática considera el
desarrollo de seis capacidades matemáticas, consideradas esenciales para el uso
instrumental de la Matemática. Éstas sustentan la competencia matemática
resolución de problemas y deben abordarse en todos los niveles y modalidades
de la Educación Básica Regular.
Estas
seis capacidades son las siguientes:
1. Matematizar
2. Representar
3. Comunicar
4. Elaborar
estrategias
5. Utilizar
expresiones simbólicas
6. Argumentar
Todas
ellas están implicadas en cualquier situación problemática real, científica o
matemática. Pueden ser utilizadas por nuestros estudiantes cada vez que las
enfrentan para resolverlas.
DEFINIENDO
LAS CAPACIDADES MATEMATICAS
1. Matematizar
La
matematización es un proceso que dota de una estructura matemática a una parte
de la realidad o a una situación problemática real. Este proceso es eficaz en
tanto pueda establecer un isomorfismo, es decir, igualdad en términos de
formas entre la estructura matemática y la realidad. Cuando esto ocurre las
propiedades de la estructura matemática corresponden a la realidad y
viceversa.
Matematizar
Implica también interpretar una solución matemática o un modelo matemático a
la luz del contexto de una situación problemática.
POR
EJEMPLO:
Los sistemas de numeración
tuvieron un origen anatómico. Nuestros antepasados valiéndose de los dedos de
sus manos contaban hasta diez; uno/huk/, dos/iskay/, tres/ kimsa/,
cuatro/tawa/,cinco/pichqa/, seis/suqta/, siete/qanchis/, ocho/pusaq/, nueve/isqun/
y diez/chunka).
Al llegar a diez /chunka/, es decir, después de consumir todas
las posibilidades de su «aparato de cálculo» natural, los dedos de sus dos
manos, les fue lógico considerar el número 10 como una unidad nueva, mayor (la
unidad del orden siguiente) y prosiguieron el contero en los términos
siguientes: diez y uno/chunka hukniyuq/, diez y dos /chunka iskayniyuq/, diez y
tres /chunka kimsayuq/, diez y cuatro/chunka tawayuq/, diez y cinco /chunka
pichkayuq/, diez y seis /chunka suqtayuq/, diez y siete /chunka qanchikniyuq/,
diez y ocho / chunka pusaqniyuq/, diez y nueve/chunka isqunniyuq/ y dos veces
diez (veinte)/iskay chunka/.
“El conteo a base de los dedos de
las dos manos dio origen al sistema de numeración decimal quechua. Nuestros
antepasados dotaron de una estructura matemática decimal a una parte de su anatomía,
sus dos manos y nos legaron el sistema de numeración decimal quechua”
Al llegar a veinte, formaban la segunda decena y proseguían
el conteo hasta llegar a diez decenas /chunkachunka/ y asílograban formar la
unidad del tercer orden, la centena /pachak/ y así sucesivamente.
Algo similar, sucedió probablemente con nuestros antepasados
aimaras. Ellos, a diferencia de los quechuas, se valieron de los dedos sólo de
una de sus manos, y contaban con facilidad hasta llegar a cinco (uno /maya/,
dos/paya/, tres/kima/, cuatro/pusi/ y cinco/qallqu/) Al llegar a cinco, les fue
lógico considerar el número 5 como una unidad nueva, mayor (la unidad del orden
siguiente) y prosiguieron el contero en los términos siguientes: uno y cinco
/ma-qallqu/, dos y cinco / pa-qallqu/, tres y cinco /ki-qallqu/, cuatro y
cinco/pu-qallqu/ y cinco y cinco/qallqu qallqu.
Al llegar a cinco y cinco,
formaban la unidad del segundo orden, después de tercer orden y así
sucesivamente. Así los aimaras dotaron de una estructura matemática quinaria a
una de sus manos y nos legaron el sistema de numeración quinaria aimara. Así
matematizaron nuestros antepasados porciones o partes de su anatomía.
“Matematizar implica,
entonces, expresar una parcela de la realidad, un contexto concreto o una
situación problemática, definido en el mundo real, en términos matemáticos”
2. Representar
Existen
diversas formas de representar las cosas y, por tanto, diversas maneras de
organizar el aprendizaje de la matemática. El aprendizaje de la matemática es
un proceso que va de lo concreto a lo abstracto. Entonces, las personas, los
niños en particular, aprendemos matemática con más facilidad si construimos
conceptos y descubrimos procedimientos matemáticos desde nuestra experiencia
real y particular. Esto supone manipular materiales concretos (estructurados o
no), para pasar luego a manipulaciones simbólicas. Este tránsito de la
manipulación de objetos concretos a objetos abstractos está apoyado en nuestra
capacidad de representar matemáticamente los objetos.
“La capacidad de representar es
fundamental no solo para enfrentar situaciones problemáticas, sino para
organizar el aprendizaje de la matemática y socializar los conocimientos
matemáticos que los estudiantes vayan logrando”
POR
EJEMPLO:
Cuando
enfrentamos a una situación problemática real susceptible de matematización,
la representamos matemáticamente. Para eso utilizamos distintas
representaciones tales como: gráficos, tablas, diagramas, imágenes, etc. Así
capturamos y describimos la estructura y las características matemáticas de
una determinada situación.
Cuando
ya disponemos de resultados matemáticos, presentados en diversos formatos o
representaciones matemáticas, los interpretamos. Para hacer esa interpretación
nos referimos a la situación problemática y usamos las representaciones para
resolverla. A veces es necesario crear nuevas representaciones.
3. Comunicar
El lenguaje matemático es también una
herramienta que nos permite comunicarnos con los demás. Incluye distintas
formas de expresión y comunicación oral, escrita, simbólica, gráfica. Todas
ellas existen de manera única en cada persona y se pueden desarrollar en las
escuelas si éstas ofrecen oportunidades y medios para hacerlo.
Buscamos
desarrollar esta capacidad en los estudiantes para que logren comprender
desarrollar y expresar con precisión matemática las ideas, argumentos y
procedimientos utilizados, así como sus conclusiones. Asimismo, para
identificar, interpretar y analizar expresiones matemáticas escritas o verbales.
En
matemáticas se busca desarrollar en los estudiantes esa capacidad para recibir,
producir y organizar mensajes matemáticos orales en forma crítica y creativa.
Esto les facilita tomar decisiones individuales y grupales.
La institución educativa debe brindar
situaciones reales de interacción oral para que los estudiantes tengan
oportunidad de hablar, dialogar, opinar, informar, explicar, describir, argumentar,
debatir, etc., en el marco de las actividades matemáticas programadas.
La lectura y el dar sentido a las
afirmaciones, preguntas, tareas matemáticas, permiten a los estudiantes crear
modelos de situaciones problemáticas, lo cual es un paso importante para
comprender, clarificar, plantear y resolverlas en términos matemáticos.
“La gran cantidad de
información matemática que se dispone re quiere desarrollar en los estudiantes
la capacidad de comunicación escrita. Eso les posibilita identificar, procesar,
producir y administrar información matemática escrita. El lenguaje matemático
escrito constituye el medio de comunicación más eficaz”
4. Elaborar
estrategias
Al
enfrentar una situación problemática de la vida real, lo primero que hacemos es
dotarla de una estructura matemática. Luego, seleccionamos una alternativa de
solución entre otras opciones. Sino disponemos de ninguna alternativa
plausible, intentamos crearla. Entonces, cuando ya disponemos de una
alternativa razonable de solución, elaboramos una estrategia.
De esta manera, la resolución de una
situación problemática supone la selección o elaboración de una estrategia para
guiar el trabajo, interpretar, evaluar y validar su procedimiento y solución
matemáticos. La construcción de conocimientos matemáticos requiere también
seleccionar o crear y diseñar estrategias de construcción de conocimientos.
POR
EJEMPLO:
Un avión sube a una altura de 2 000 metros,
después baja 1 300 metros, vuelve a subir 1500 metros y baja de nuevo 250 metros.
¿A qué altura se encuentra en este momento?
“La capacidad de
elaborar estrategias es fundamental para construir conocimientos matemáticos, y
también para resolver situaciones problemáticas”
5. Utilizar
expresiones simbólicas
Hay
diferentes formas de simbolizar. Éstas han ido construyendo sistemas simbólicos
con características sintácticas, semánticas y funcionales peculiares.
El uso de las expresiones y símbolos
matemáticos ayudan a la comprensión de las ideas matemáticas, sin embargo
estas no son fáciles de generar debido a la complejidad de los procesos de
simbolización.
En el desarrollo de los aprendizajes matemáticos,
los estudiantes a partir de sus experiencias vivenciales e inductivas emplean
diferentes niveles del lenguaje. Inicialmente usan un lenguaje de rasgos coloquiales,
paulatinamente van empleando el lenguaje simbólico hasta llegar a un lenguaje
técnico y formal como resultado de un proceso de convención y acuerdo en el
grupo de trabajo.
Al
dotar de estructura matemática a una situación problemática, necesitamos usar
variables, símbolos y expresiones simbólicas apropiadas. Para lograr esto es
importante:
·
Entender
la relación entre el lenguaje del problema y el lenguaje simbólico necesario
para representarlo matemáticamente.
·
Comprender,
manipular y hacer uso de expresiones simbólicas—aritméticas y
algebraicas—regidas por reglas y convenciones matemáticas, es decir, por una
gramática específica de lenguaje matemático.
“La capacidad de usar símbolos y
expresiones simbólicas es indispensable para construir conocimientos y resolver
problemas matemáticos. Pero también para comunicar, explicar y entender
resultados matemáticos”
6. Argumentar
Esta
capacidad es fundamental no solo para el desarrollo del pensamiento matemático,
sino para organizar y plantear secuencias, formular conjeturas y
corroborarlas, así como establecer conceptos, juicios y razonamientos que den
sustento lógico y coherente al procedimiento o solución encontrada.
Así,
se dice que la argumentación puede tener tres diferentes usos:
1. Explicar
procesos de resolución de situaciones problemáticas
2. Justificar, es
decir, hacer una exposición de las conclusiones o resultados a los que se haya
llegado
3. Verificar
conjeturas, tomando como base elementos del pensamiento matemático.
La
capacidad de argumentar se aplica para justificar la validez de los resultados
obtenidos. El diálogo colectivo basado en afirmaciones u opiniones
argumentadas, así como el análisis de la validez de los procesos de resolución
de situaciones problemáticas favorecen el aprendizaje matemático. En la
Educación Básica, se procura que los estudiantes:
·
Hagan
progresivamente inferencias que les permita deducir conocimientos a partir de
otros, hacer predicciones eficaces en variadas situaciones concretas, formular
conjeturas e hipótesis.
·
Aprendan
paulatinamente a utilizar procesos de pensamiento lógico que den sentido y
validez a sus afirmaciones, y a seleccionar conceptos, hechos, estrategias y
procedimientos coherentes.
- Desarrollen
la capacidad para detectar afirmaciones y justificaciones erróneas.
El
razonamiento y la demostración son partes integrantes de la argumentación.
Entran en juego al reflexionar sobre las soluciones matemáticas y permiten
crear explicaciones que apoyen o refuten soluciones matemáticas a situaciones
problemáticas contextualizadas.
“Razonar implica reflexionar sobre
los mecanismos lógicos e intuitivos que hacen posible conectar diferentes
partes de la información. Esto permite llegar a una solución plausible,
analizar e integrar la información, para construir o sostener argumentos,
justificar y validar la toma de decisiones, para hacer generalizaciones y
combinar múltiples elementos de información”
DOMINIOS
MATEMÁTICOS
Los dominios son los organizadores del Área
de Matemática, que se trabajan a lo largo de la Educación Básica y que en
algunos momentos puede haber un mayor énfasis en un dominio que en otro. Estos
dominios son:
1. Números y
Operaciones
Se
refiere al conocimiento de números, operaciones y sus propiedades. Este
dominio dota de sentido matemático a la resolución de situaciones problemáticas
en términos de números y operaciones.
La
situación sirve de contexto para desarrollar capacidades matemáticas mediante
la construcción del significado y uso de los números y las operaciones en cada
conjunto numérico, y en diversas formas a fin de realizar juicios matemáticos y
desarrollar estrategias útiles en diversas situaciones.
2. Cambio y
Relaciones
Se
refiere a conocimientos algebraicos tales como ecuaciones, inecuaciones,
relaciones, funciones, sus propiedades, entre otros.
Este dominio dota de sentido matemático a
la resolución de situaciones problemáticas en términos de patrones, equivalencias
y cambio la misma que sirve de contexto para desarrollar las capacidades
matemáticas.
El
mundo que nos rodea presenta una multiplicidad de relaciones temporales o
permanentes, que se manifiestan por ejemplo en los diversos fenómenos
naturales, económicos, demográficos entre otros. Ellos influyen en la vida de
todo ciudadano, exigiéndole capacidades que le permitan comprenderlos,
describirlos, analizarlos, modelarlos y realizar predicciones para enfrentarse
a los cambios. Así se aligeran o reducen sus consecuencias (OCDE, 2006).
En
este contexto resulta importante el aporte de la matemática a través de la
matematización, Ella permite analizar las soluciones de un problema,
generalizarlas y justificar su alcance. A medida que se desarrolla esta
capacidad se va progresando en el uso del lenguaje y el simbolismo matemático,
necesarios para apoyar y comunicar el pensamiento algebraico por medio de
ecuaciones, variables y funciones.
“El álgebra no es solo un medio de traducción del
lenguaje natural al simbólico, es también una herramienta de matematización de
distinta s situaciones de la vida real. Por eso, los estudiantes necesitan
aprender a identificar regularidades, comprender el concepto de igualdad y
analizar el cambio de situaciones que van incorporando paulatinamente el uso de
códigos, símbolos y funciones”
La
resolución de situaciones problemáticas sobre cambio y relaciones permite
desarrolla la capacidad para identificar patrones, describir y caracterizar
generalidades, modelar fenómenos reales referidos a las relaciones cambiantes
entre dos o más magnitudes. Para eso se puede utilizar desde gráficos
intuitivos hasta expresiones simbólicas como las igualdades, desigualdades,
equivalencias y funciones.
3. Geometría
Se
refiere a conocimientos de la geometría y a sus propiedades. Este dominio dota
de sentido geométrico a la resolución de situaciones problemáticas, la misma
que sirve de contexto para desarrollar capacidades matemáticas.
En
efecto, vivimos en un mundo que está lleno de formas y cuerpos geométricos. A
nuestro alrededor podemos encontrar evidencias geométricas en la pintura, la
escultura, las construcciones, los juegos, las plantas, los animales y en diversidad
de fenómenos naturales.
“El aprendizaje de la geometría
pasa del reconocimiento y análisis de las formas y sus relaciones hasta la
argumentación formal y la interrelación entre distintos sistemas geométricos.
Por eso conviene aprender geometría desarrollando capacidades para visualizar,
comunicar, dibujar, argumentar y modelar”
Estas situaciones del mundo real demandan
de la persona, poner en práctica capacidades entorno a la geometría como
obtener información a partir de la observación; interpretar, representar y
describir relaciones entre formas, desplazarse en el espacio, entre otras.
Aprender geometría proporciona a la persona herramientas y argumentos para
comprender su entorno. La geometría es considerada como una herramienta para
el entendimiento y, es la parte de las matemáticas más intuitiva, concreta y
ligada a la realidad(Cabellos Santos, 2006).
La
resolución de situaciones problemáticas sobre geometría permite desarrollar
progresivamente la capacidad para:
·
Describir
objetos, sus atributos medibles y su posición en el espacio utilizando un
lenguaje geométrico
·
Comparar y
clasificar formas y magnitudes
·
Graficar
el desplazamiento de un objeto en sistemas de referencia
·
Componer y
descomponer formas
·
Estimar
medidas, utilizar instrumentos de medición
·
Usar
diversas estrategias de solución de problemas
4.
Estadística y Probabilidad
Se
refiere a conocimientos de la estadística y la probabilidad, y a sus
propiedades. Este dominio dota de sentido matemático a la resolución de
situaciones problemáticas en términos estadísticos y probabilísticos, la misma
que sirve de contexto para desarrollar capacidades matemáticas.
La
incertidumbre está presente en nuestra vida cotidiana, somos testigos que raras
veces las cosas ocurren según las predicciones realizadas.
POR
EJEMPLO:
Los
pronósticos del tiempo o el resultado de las elecciones a veces nos traen
sorpresas. La ciencia y la tecnología rara vez se ocupan de las certidumbres,
pues el conocimiento científico casi nunca es absoluto e incluso puede ser
erróneo en algunas ocasiones.
Los
aprendizajes que se logran a partir de la Estadística y el cálculo de
probabilidades adquieren hoy mayor importancia de la que tenían en el pasado6 , pues son herramientas que ayudan al
estudiante a organizar y profundizar su conocimiento sobre la realidad,
permitiéndole tomar decisiones en escenarios de cambio y de abundante
información.
La resolución de situaciones problemáticas
sobre estadística y probabilidad permite desarrollar progresivamente
capacidades para procesar e interpretar diversidad de datos, transformándolas
en información. También ayuda a analizar situaciones de incertidumbre para
estimar predicciones, que permita tomar decisiones adecuadas.
“El aprendizaje de la
estadística y la probabilidad permite al estudiante reconocer los alcances y
limitaciones de la matemática y reconocer q u e la solución de los problemas no
es s empre única o inmediata, sino que existe una fuerte presencia de fenómenos
aleatorios.
Las capacidades matemáticas:
- Aparecen y se desarrollan de manera natural
sin un orden pre establecido.
- Se interrelacionan y complementan.
- Se pueden desarrollar de manera simultánea.
- Están articuladas por el conocimiento
matemático.
- Las capacidades facilitan el desarrollo
de la competencia.
ESCENARIOS MATEMATICOS
1. LABORATORIO MATEMATICO,
- Es un espacio de aprendizaje donde a través de
técnicas inductivas el niño va descubriendo regularidades matemáticas.
- El estudiante tiene la oportunidad de vivenciar
y experimentar de manera lúdica los conceptos y propiedades matemáticas.
2. TALLER MATEMATICO
- Es un espacio de puesta en práctica de
habilidades y destrezas ya logradas,
y puede transferir a nuevas
situaciones.
- Se usan diversas estrategias y recursos (procedimentales, cognitivos y actitudinales) orientadas a resolver situaciones problematicas
3. PROYECTO
- Es un espacio de aprendizaje que acerca al niño
a resolver situaciones del contexto social, cultural, económico y
ecológico.
- Los estudiantes aprenden actuando en la
realidad, con continua autorreflexión.
ESCENARIOS PARA EL
DESARROLLO DE LA COMPETENCIA MATEMATICA
CARACTERISTICAS DE LOS
ESCENARIOS
SEMEJANZAS Y DIFERENCIAS DE
LOS ESCENARIO
CUADRO COMPARATIVO DE CAPACIDADES Y COMPETENCIAS POR CICLOS
Atte.
Edgar Zavaleta Portillo
IE. Humberto Luna-Ugel cusco















Hola, soy profesor universitario de Matemáticas acá en México, me pareció muy interesante su descripción de las competencias matemáticas, coincido en que buscamos hacer las matemáticas más cercanas a los alumnos haciéndoles la actividad matemática más significativa para contextos reales
ResponderEliminar